[프로그래머스] 디스크 컨트롤러 - 힙 (Heap) Level 3 (Java)

[프로그래머스] 디스크 컨트롤러 (Java)

힙 (Heap) - Level 3

 

 

👉 문제 링크

코딩테스트 연습 - 디스크 컨트롤러

👉 문제 풀이 전체 소스 (github)

GitHub - jennie267/algorithm: 알고리즘

 

 

문제 설명

하드디스크는 한 번에 하나의 작업만 수행할 수 있습니다. 디스크 컨트롤러를 구현하는 방법은 여러 가지가 있습니다. 가장 일반적인 방법은 요청이 들어온 순서대로 처리하는 것입니다.

예를들어

- 0ms 시점에 3ms가 소요되는 A작업 요청
- 1ms 시점에 9ms가 소요되는 B작업 요청
- 2ms 시점에 6ms가 소요되는 C작업 요청

와 같은 요청이 들어왔습니다. 이를 그림으로 표현하면 아래와 같습니다.

 

 

한 번에 하나의 요청만을 수행할 수 있기 때문에 각각의 작업을 요청받은 순서대로 처리하면 다음과 같이 처리 됩니다.

 

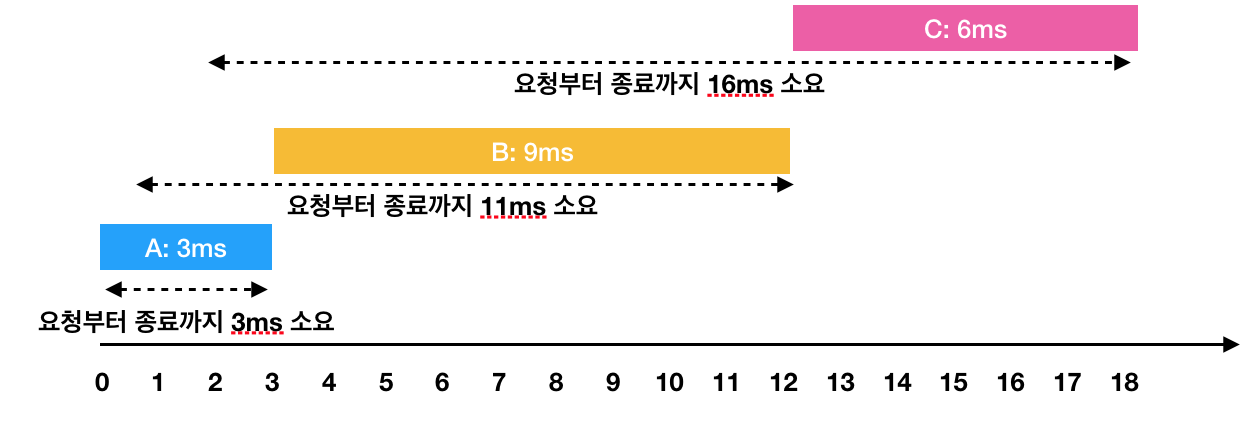
- A: 3ms 시점에 작업 완료 (요청에서 종료까지 : 3ms)
- B: 1ms부터 대기하다가, 3ms 시점에 작업을 시작해서 12ms 시점에 작업 완료(요청에서 종료까지 : 11ms)
- C: 2ms부터 대기하다가, 12ms 시점에 작업을 시작해서 18ms 시점에 작업 완료(요청에서 종료까지 : 16ms)

 

이 때 각 작업의 요청부터 종료까지 걸린 시간의 평균은 10ms(= (3 + 11 + 16) / 3)가 됩니다.

하지만 A → C → B 순서대로 처리하면

- A: 3ms 시점에 작업 완료(요청에서 종료까지 : 3ms)
- C: 2ms부터 대기하다가, 3ms 시점에 작업을 시작해서 9ms 시점에 작업 완료(요청에서 종료까지 : 7ms)
- B: 1ms부터 대기하다가, 9ms 시점에 작업을 시작해서 18ms 시점에 작업 완료(요청에서 종료까지 : 17ms)

이렇게 A → C → B의 순서로 처리하면 각 작업의 요청부터 종료까지 걸린 시간의 평균은 9ms(= (3 + 7 + 17) / 3)가 됩니다.

각 작업에 대해 [작업이 요청되는 시점, 작업의 소요시간]을 담은 2차원 배열 jobs가 매개변수로 주어질 때, 작업의 요청부터 종료까지 걸린 시간의 평균을 가장 줄이는 방법으로 처리하면 평균이 얼마가 되는지 return 하도록 solution 함수를 작성해주세요. (단, 소수점 이하의 수는 버립니다)

 

제한사항

 

• jobs의 길이는 1 이상 500 이하입니다.
• jobs의 각 행은 하나의 작업에 대한 [작업이 요청되는 시점, 작업의 소요시간] 입니다.
• 각 작업에 대해 작업이 요청되는 시간은 0 이상 1,000 이하입니다.
• 각 작업에 대해 작업의 소요시간은 1 이상 1,000 이하입니다.
• 하드디스크가 작업을 수행하고 있지 않을 때에는 먼저 요청이 들어온 작업부터 처리합니다.

 

 

 

 

 

입출력 예제

 

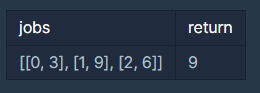
입출력 예 설명

문제에 주어진 예와 같습니다.

• 0ms 시점에 3ms 걸리는 작업 요청이 들어옵니다.
• 1ms 시점에 9ms 걸리는 작업 요청이 들어옵니다.
• 2ms 시점에 6ms 걸리는 작업 요청이 들어옵니다.

 

 

문제 풀이

import java.util.Arrays;
import java.util.Comparator;
import java.util.PriorityQueue;
class Solution {
    public int solution(int[][] jobs) {
        int size = jobs.length;
        int totTime = 0;

        Arrays.sort(jobs, (Comparator.comparingInt(o -> o[0])));
        PriorityQueue<int[]> queue = new PriorityQueue<>(Comparator.comparingInt(o -> o[1]));

        int i = 0;
        int curTime = 0;
        while (size > 0) {
            while (i < jobs.length && jobs[i][0] <= curTime) {
                queue.offer(jobs[i++]);
            }

            if (queue.isEmpty()) {
                curTime = jobs[i][0];
            } else {
                int[] request = queue.poll();
                totTime += curTime - request[0] + request[1];
                curTime += request[1];
                size--;
            }

        }
        return (int) Math.floor(totTime/jobs.length);
    }
}